Notes on antenna simulation using NEC-2
Main → Technical Articles → Notes on antenna simulation using NEC-2 |
![]() Este artículo también está disponible en español (this article is also available in Spanish).
Este artículo también está disponible en español (this article is also available in Spanish).
![]() Abstract:
Abstract:
This article summarizes some useful advices for efficient antenna simulation with programs based on the NEC-2 algorithm, developed by the Lawrence Livermore Laboratory. The advices and rules of design have been collected from the user’s manuals of some programs and from technical articles about antenna simulation. On the other hand, some guidelines to simulate multiband and wideband antennas are provided.
Article published in the Spanish Amateur Radio Union Magazine (URE). December 2012.
nec-2_ea4fsi_ure_dic2012.pdf (782 kB)
Table of contents.
1.Introduction.
2.Coordinate system.
2.1. Conventions for model representation.
3.Geometry of the models.
3.1. General rules.
3.2. Length of the segments.
3.3. Radius of the wires.
3.4. Segment density.
4.Types of ground and height of the wires.
4.1. Free space.
4.2. Perfect ground.
4.3. Fast ground.
4.4. MININEC ground.
4.5. Sommerfeld-Norton (S-N) ground.
5. Generators, loads and transmission lines.
6. Other considerations.
7. Model verification.
7.1. Convergency test.
7.2. Average gain test (AGT).
8. References.
1. Introduction.
Those notes are a collection of advices and rules of design to perform simulations of antennas with programs based on the NEC-2 algorithm. The notes are not oriented to be a guide to work with the different available programs based on this algorithm, but they pretend to be a quick reference for users already initiated on its use. The advices and rules of design have been collected from the user’s manuals of some programs and from technical articles about antenna simulation, with the references shown in the section 8.
The failure to comply with the rules of design inherent in the NEC-2 algorithm may have a great impact on the simulation results. For example, the resulting calculations of antenna impedance will very often be erroneus and the simulated radiation patterns unreal.
The NEC-2 algorithm was developed in 1981 in the United States by the Lawrence Livermore National Laboratory, with the sponsorship of the Naval Ocean Systems Center and the Air Force Weapons Laboratory [Ref.1] and is based on the method of the moments [Ref.2].
Note that some of the rules are not applicable to later versions of the algorithm (NEC3 and NEC-4), which are more advanced and whose code is not available to the public. On the other hand, take into account that not all the most known antenna simulation programs among all the available as shareware are based on this algorithm. For example, 4Nec2 and EZNEZ are based on NEC-2, but others such as MMANA-GAL are based in variations of MININEC [Ref.9].
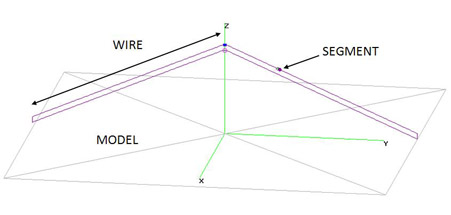
The following terminology will be used throughout this article (see fig.1):
-
Model: simulation set made up of all the radiators of the antenna (including the loads), the generator and the type of ground.
-
Wire: each of the straight conductors forming an antenna model in the programs based on NEC-2. In order to define a wire of length Lh in NEC-2, it is necessar to specify the coordinates of the two points delimiting its ends, the conductive material employed, the wire diameter Dh and the number of segments which will form the wire. Let Zs be the height of the wire over the ground. If the wire is not paralell to the ground, the height of the end nearest to the ground will be considered. We will name Ns the number of segments making up a wire.
-
Segment: each of the straight divisions making up each wire in an antenna modelled with programs based on NEC-2, being used by the algorithm for the computation of currents by means of pulses. The segments will have a length Ls, which may be specified by the user or computed automatically by some of the programs, a process named autosegmentation. The method of the moments in which NEC-2 is based on, computes the interaction between segmentss.
-
Segment density: number of segments per wavelength in a wire. Note that in the case of multiband or wideband antennas, the segment density will be different for each working frequency.
-
Wavelength: the wavelength corresponding to the working frequency of a specific simulation in a program based on NEC-2.
-
Critical zone: a part of a model presenting geometric characteristics which require special designs in order for the NEC-2 simulations to be correct.
2. Coordinate system.
The understanding of the coordinate system employed in a simulation program is fundamental both for the design of the models and to correctly evaluate the results of the simulations. The coordinate systems may be different among the different programs based on NEC-2. The fig.2 shows the coordinate system used in 4Nec2.
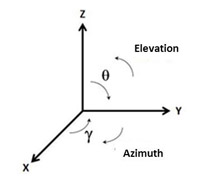
The ground is simulated in the XY plane and the Z axis represents the height over the ground.
The following angles are defined:
-
Theta: angle measured between the positive Z semiaxis and the ground plane XY. In this manner, the ground plane may be defined as the plane Theta=90 degrees.
-
Phi: angle measured between the positive X semiaxis and the YZ plane.
-
Elevation: angle measured between the ground plane XY and the positive Z semiaxis. An elevation of 90 degrees will correspond to the perpendicular to the ground plane.
-
Azimuth: angle measured in parallel planes to the ground plane XY. The azimuth angles are measured clockwise from the Y axis towards the X axis. The Y axis has an azimuth of zero degrees.
2.1. Conventions for model representation.
In order to make possible the comparison of the radiation patterns os different antennas in an easy way, it is advisable that all the models are represented geometrically agreeing with a set of general conventions. In this section, an example of conventions gathered from [Ref.5] are shown:
-
If the model includes ground, it will be located in the XY plane.
-
The Z axis will represent the height of the antenna over the ground plane XY.
-
All the linear elements of the antenna will be represented in the Y axis or in other axes parallel to the Y axis.
-
The X axis will be used for the front-to-back direction. For isolated elements, we will establish X=0.
-
If the model has symmetry, as far as possible the axes of the coordinate system will be used as axes of symmetry.
3. Geometry of the models.
Before defining the structure of a model in NEC-2, it is necessary to consider in which way the current flows are managed in each simulation program. For example, in 4Nec2 the positive current always flows from the end 1 to the end 2 of each wire.
On the other hand, it is necessary to observe the geometric rules presented in the next sections.
3.1. General rules.
In order to avoid errors, it is of interest to observe the following general rules while designing simulation models:
-
Two wires may not meet in the intermediate points of any of their segments [Ref.5].
-
In a model with several wires, it is advisable not to connect short segments with long segments [Ref.4]. Some programs may impose conditions in this regard. For example, in 4Nec2, for two connected segments “i” and “j” the condition Lsi <= 5 x Lsj must be fulfilled [Ref.7].
-
The angle formed by two joint segments, their length and their diameter must be configured in such a way that the (1/3) centerparts of both segments do not overlap [Ref.4,8].
-
Two parallel or near parallel wires very close of each other must have their segments aligned [Ref.3,4] and must have the same kind of segmentation [Ref.7]. It is advisable for the distance between them to be at least several wire diameters as well [Ref.8].
-
If two wires of different diameters are close of each other, despite the fact that their segments are aligned, errors in the computation of the antenna gain and its input impedance may be obtained, especially in the part of the reactance [Ref.5,11]. In models of those characteristics it is advisable to perform the AGT test (see section 7.2) in order to check their validity.
-
If two wires of different diameters join in a point, the results of the simulations may not be precise [Ref.5]. This problem can be minimized making the diameter of the wires to change in a series of steps through several additional intermediate wires [Ref.3].
-
NEC-2 allows to join up to around 30 angularly equispaced wires in the same point [Ref.3], for example in order to simulate a plane of radials. It is not advisable to employ a higher number because the angle between each pair of wires would be small and the results of NEC-2 would lose precision [Ref.5].
3.2. Length of the segments.
Para mejorar los resultados de las simulaciones y salvo en zonas críticas de los modelos, es recomendable que todos los segmentos de un modelo tengan la misma longitud [In order to get better results in the simulations and apart from the critical zones of the models, it is advisable that all the segments of a model have the same length [Ref.4,5].
Regarding the minimum length of the segments (Lsmin), in the different references checked the following restrictions related to the diameter of the wire and the wavelength have been found:
-
[Ref.8]: Lsmin > Dh
-
[Ref.4]: Lsmin > 2 x Dh
-
[Ref.5]: Lsmin > 4 x Dh
-
[Ref.7,10]: Lsmin > (lambda/10000)
In regards of the maximum length of the segments (Lsmax), the following restrictions related to the wavelength are specified
-
[Ref.4,7]: Lsmax < (Lambda / 20)must be observed at least in the critical zones.
-
[Ref.7,10]: Lsmax < (lambda / 10) will be enough for most cases, being possible to use even Lsmax < (lambda / 5) for segments integrated in long wires without critical zones.
3.3. Radius of the wires.
According to our terminology, the wire radius is defined by (Dh/2). Restrictions related to the minimum and maximum radius of the wires, as a function of the length of the segments, may be imposed in some programs. For example:
-
[Ref.7]: in 4Nec2, the proportion (Dh/2) < (Ls/10) must be observed.
3.4. Segment density.
Under normal circumstances, the higher the segment density, the better results will be obtained in the simulations, with the cost of a higher computing time. Nevertheless, if a model is already precise enough, an increase of the segment density will not provide further improvements.
On the other hand, it is necessary to take into account that if the total number of segments in a model is very high, the maximum limit which some programs may impose can be reached [Ref.9].
One wire must have at least 8-10 segments per each semi-wavelength [Ref.5,8]. If this rule is not observed, the results won’t be precise, especially those related to the computation of the input impedance of the antenna. If a wire is a quarter-wavelength long, 5 segments will be a good minimum [Ref.5].
In the case of multiband or wideband antennas, the segment density will be different for each working frequency. Therefore, the number of segments employed must be changed with the frequency, or must be calculated in order to be above the recommended minimum corresponding to the highest working frequency (lower wavelength) [Ref.8].
In order to determine the optimum segment density, it is interesting to perform a convergency test (see section 7.1).
4. Types of ground and height of the wires.
In this section, the characteristics of the different types of ground available in most programs implementing the NEC-2 algorithm are described. For each case, specifications are provided regarding whether the wires may touch ground or not and in the negative case at which height over ground must be placed.
In every case apart from the free space, it is necessary to take into account the diameter of the wires: the minimum height of a horizontal wire over the ground must be at least twice the diameter of that particular wire:
-
[Ref.4]: Zs > 2 x Dh
4.1. Free space.
In the simulations in free space, logically there is no ground. Normally, the results will be similar to those one may find in the textbooks.
4.2. Perfect ground.
The perfect ground consists of a perfect electrical conductor ground plane, without losses. It is a good option to make simulations omitting the losses of the ground, a task which may allow to evaluate those losses comparing the results with further simulations using more realistic ground types.
The wires of a model can touch the perfect ground .
4.3. Fast ground.
With the fast ground type, NEC-2 uses a method based on complex reflection coefficients.
The wires of the model cannot touch the fast ground.
In the case of the horizontal wires, it is necessary to observe a height over the ground of at least one tenth of the working wavelength
-
[Ref.4,8]: Zs > (lambda / 10) for horizontal wires.
4.4. MININEC ground.
The MININEC ground model assumes a perfect ground for the computation of the currents and changes to a dielectric ground for the computation of the far field patterns (ground without losses). With the MININEC ground, hybrid calculations designed for the first generation of less powerful computers are used.
The vertical wires can touch the MININEC ground.
The horizontal wires cannot touch the ground. They must be placed at a height over the ground of at least one fifth of the working wavelength:
-
[Ref.4,8]: Zs > (lambda / 5) for horizontal wires over MININEC ground.
If this rule is not observed, the simulations with NEC-2 will provide as a result erroneus impedances and anomalous high gains, especially for horizontal polarization.
4.5. Sommerfeld-Norton (S-N) ground.
The Sommerfeld-Norton (S-N) is the most precise ground model, with the highest computational cost and is the best method to simulate horizontal wires very close to the ground.
Using the S-N ground it is important to take into account that both the vertical and the horizontal wires cannot touch ground.
One way to simulate a connection of a vertical wire to the ground is by means of a virtual plane of at least eight radials [Ref.7], taking into account that the electrical conductivity characteristics of the simulated ground will be modified and therefore that the results may be inaccurate.
In the references checked, the following rules related to the height of the horizontal wires have been found:
-
[Ref.4]: Zs > (lambda / 200)
-
[Ref.5,8]: Zs > (lambda / 1000)
5. Generators, loads and transmission lines.
This section shows some advices and rules of design about the characteristics of the generators, loads and transmission lines to be used in the simulations.
The loads and transmission lines used in NEC-2 are mathematical models instead of physical models. Therefore, they do not contribute to the radiation of the antenna [Ref.5,8]. If it is considered that the transmission line may have influence on the radiation of the real antenna which is being simulated, it is possible to try to create a model of the line in some particular cases, such as with the parallel transmission line.
As a general rule, a generator of complex value 1 +j0 will be adequate for most of the simulations [Ref.4,5]. In the simulation of arrays, it may be necessary to use several generators phase shifted. See an example in the article “Adcock/Watson-Watt Radio Direction Finding”.
Take into account that it is not allowed to use generators or loads in the ends of wires in open circuit [Ref.7,11]. The generator would see load in one of its poles and open circuit in the other one, so theoretically there would not be current generated in any way. In the simulations, the input impedance of the antenna would be erroneous, reaching too high values (especially in the reactive part) and a too low level current would be generated through the mutual coupling between the part of the generator connected to the antenna and the piece of segment connected to the other pole of the generator, which remains in open circuit.
If the generator is to be placed in the center of a wire, it is recommended to model this wire with an odd number of segments [Ref.5], so there will be a symmetrical distribution of currents in the wire.
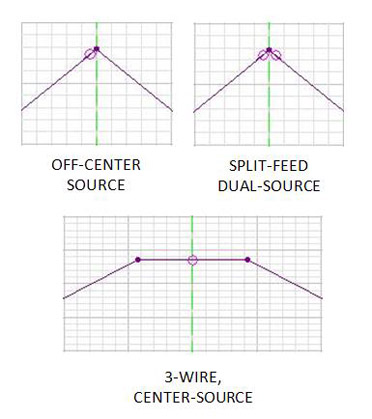
If a generator is to be placed in the apex formed by two wires joining with an angle different from 180 degrees, such as in the case of inverted-vee antennas, several techniques can be used [Ref.3,5,6,8,10] as shown in the fig.3
-
Off-center source: the less precise option consists in placing only one generator in one of the wires. The distribution of currents may be asymmetric and the values of the input impedance of the antenna may be inaccurate. The precision may be improved using the technique of “segment tappering”, dividing each wire in several concatenated wires and making those closest to the generator to have shorter segments, in a way that the generator is placed close to the apex.
-
Split-feed / Dual source: this technique consists in using two generators (one on each of the final segments of the wires joining in the apex) of half the voltage which would be used with only one generator. It is interesting to configure a high segment density in order for those generators to be very close to the apex.
-
3-wire, center source: finally, the most precise technique consists in joining both wires with a third additional small wire with three segments and placing the generator in the central segment of the latter. This is the most precise technique from the point of view of the simulation of the impedance of the antennas, provided that the length of the three segments of the additional wire is similar to the length of the segments of the two main wires.
6. Other considerations.
This section shows other advices and rules of design not related to the previous sections:
-
The method of the moments [Ref.2] is adequate for the simulation of antennas with thin wires. The simulation of thick wires may be problematic, especially in the VHF/UHF bands [Ref.8].
-
NEC-2 lacks the capacity to model dielectrics, such as underground radials or antennas with electrically isolated wires (twin-lead J-pole, twin-lead folded dipole) [Ref.4].
-
Take into account that NEC-2 computes the total current in the antenna, without making differences between common mode currents and differential mode currents [Ref.4].
-
In all the radiation patterns calculated with NEC-2, the gain is expressed in dBi.
-
NEC-2 does not allow to model underground wires [Ref.5,11].
-
NEC-2 is not adequate to model small size loop antennas (perimeter lower than 0.05 wavelengths) because in the simulations the input impedance of the antenna would result in zero or negative values [Ref.11].
7. Model verification.
Once the model has been defined, some programs implementing the NEC-2 algorithm provide options for geometric validation in order to look for non-connected wires or incorrect crossings, as well as segment validation options to verify whether the rules described in the previous sections are observed. It is interesting to perform both validations before continuing with the convergency and average gain tests.
In the case of wideband or multiband antennas operating between a minimum frequency Fmin and a maximum frequency Fmax, I suggest the following strategy of design, for example with the help of a spreadsheet
-
Once the geometry of the antenna is defined, number the wires, identifying also their diameter Dh(i) and their length Lh(i). For each of the wires “i”, perform the tasks described below.
-
Considering the frequency Fmin, compute the lengths Lsmin(Fmin) and Lsmax(Fmin) for the segments of that particular “i” wire (see section 3.2), considering whether the wire will be in a critical zone or not as well.
-
Considering the frequency Fmax, compute the lengths Lsmin(Fmax) and Lsmax(Fmax) for the segments of that particular “i” wire (see section 3.2), considering whether the wire will be in a critical zone or not as well.
-
For Fmin, determine the minimum number of segments Nmin(Fmin), taking into account both the number of segments per semi-wavelength criterion and the calculation Lh(i)/Lsmax(Fmin).
-
For Fmin, determine the maximum number of segments Nmax(Fmin), calculating Lh(i)/Lsmin(Fmin).
-
For Fmax, determine the minimum number of segments Nmin(Fmax), taking into account both the number of segments per semi-wavelength criterion and the calculation Lh(i)/Lsmax(Fmax).
-
For Fmax, determine the maximum number of segments Nmax(Fmax), calculating Lh(i)/Lsmin(Fmax).
-
The number of segments allowed for the “i" wire, Ns(i), will be inside the range [Nmin(Fmax), Nmax(Fmin)]. Get the optimum final value performing the convergency test shown if the next section.
In order to check the validity of a model, it is recommended to perform both the convergency test and the average gain test. Using just one of the tests does not ensure that the model will be adequate [Ref.8].
7.1. Convergency test.
The convergency test allows to determine the optimum number of segments to be used in a particular model.
It consists in making several simulations of the same model, increasing the number of segments by 50% (less percentage if it is not possible to observe the geometric rules) on each simulation and making a note of the maximum gain and the input antenna impedance at each step. The optimum segmentation level will be achieved at the step where no significant changes in both parameters are seen [Ref.5,8]. Once reached this point, it doesn’t make sense to use a higher number of segments because the results won’t be improved and more computation time will be used.
For each configuration of number of segments to be tested, perform a segment validation test with your program before making the convergency test.
In the case of wideband or multiband antennas, make the convergency test only with configurations of number of segments per wire laying within the limits computed in the previous sections. It doesn’t make sense to test other different configurations because geometric errors would occur. Before making the convergence test with each possible configuration of number of segments, make a segment validation in the minimum and maximum frequencies of the antenna’s working band, as a double precaution to avoid problems with the geometric rules. The convergency test must be repeated in a representative set of frequencies from all the working band of the antenna. Following the test’s results, it is possible to reach a situation where different configurations of number of segments for different sets of frequencies within the working band of the antenna must be used in the simulations.
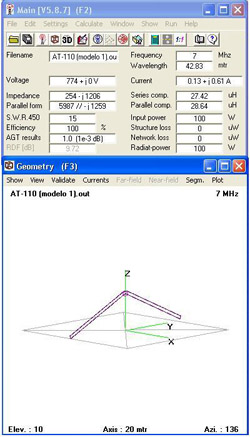
7.2. Average gain test (AGT).
The average gain test is an useful tool to check the validity of a model and it is available in practically all the programs implementing NEC-2. See the fig.4.
The AGT consists in placing the model, without loads and transmission lines, in the free space (horizontal antennas) or over perfect ground (vertical antennas) and then to simulate the 3D radiation pattern.
In theory, the average gain of a lossless antenna, considering an adequate sampling in all the possible directions of radiation, must be equal to 1. That is, the antenna must radiate all the power provided by the generator [Ref.5,8]. If this rule is not observed, the model probably has defects in the specifications of the generator or maybe the generator is located in the wrong place.
The results of the AGT are interpreted in this way [Ref.7]
-
AGT < 0.80: the model is questionable and should be refined.
-
0.80 <= AGT < 0.90: the model may be useful, but can be improved.
-
0.90 <= AGT < 0.95: the model is usable for most purposes.
-
0.95 <= AGT < 1.05: the model is likely to be accurate.
-
1.05 <= AGT < 1.10: the model is usable for most purposes.
-
1.10 <= AGT <= 1.20: the model may be useful, but can be improved.
-
AGT > 1.20: the model is questionable and should be refined.
In the case of wideband or multiband antennas, repeat the convergency test in a representative set of frequencies within all the working band of the antenna.
8. References.
-
J.G. BURKE, A.J. POGGIO et al. "Numerical Electromagnetics Code (NEC) - Method of Moments. Part II: Program Description - Code". Lawrence Livermore Laboratory. Enero 1981. Enlace.
-
R.P. HAVILAND, W4MB. “Programs for Antenna Analysis by the Method of Moments”. ARRL Antenna Compendium Vol.4. ARRL, 1995.
-
J.G. BURKE, A.J. POGGIO et al. "Numerical Electromagnetics Code (NEC) - Method of Moments. Part III: User's Guide". Lawrence Livermore Laboratory. Enero 1981. Enlace.
-
S. STEARNS, K6OIK (Northrop Grumman Electromagnetic Systems Laboratory). "Antenna Modeling for Radio Amateurs". ARRL Pacificon Antenna Seminar, San Ramon, CA. Octubre 2008. Enlace.
-
L.B. CEBIK, W4RNL. "A Beginner’s Guide to Modeling with NEC". QST, Noviembre 2000 a Febrero 2001. American Radio Relay League. Enlace.
-
L.B. CEBIK, W4RNL. "Dipoles: Variety and Modeling Hazards. Linear, V and Folded Dipoles in NEC". Antennex Monthly Columns - Antenna Modeling 207. Enlace.
-
A. VOORS. "4Nec2 General Help". Enlace.
-
Varios autores. "Antenna Modeling & System Planning". The ARRL Antenna Book. 21st edition. Newington: ARRL, 2010. p.4-1/4-18.
-
R. LEWALLEN, W7EL. "MININEC: The Other Edge of the Sword". QST, Febrero 1991. American Radio Relay League.
-
L.B. CEBIK, W4RNL. "V Arrays and Beams". Long Wire Notes. AntenneX Online Magazine, 2006.
-
R. LEWALLEN, W7EL. "EZNEC v.5.0 User Manual". Enlace.
Version 2 (Aug 2012).
Ismael Pellejero - EA4FSI |